2025-07-05

ICPC 2025 国内予選参加記（チーム Magical Fish / miscalc 視点）

はじめに

2025/7/4(金) に行われた ICPC 2025 国内予選で 7 位となり、アジア地区に進出することができました！ずっと念願だったのでめちゃくちゃ嬉しい。

チームメンバー

全員が計数 → 情報理工の数理情報学専攻 M1（ラストイヤー！）。ちなみに confeito と私は研究室まで同じ。

confeito：AtCoder のレートが 2300 くらい（昨年比 +200）とチームの中で最も高い。ARC が得意。幾何ができる貴重な人材。提出前の確認がかなり慎重で助かっている。とても頼りになる。
serendipity_：AtCoder のレートが 2100 くらい（昨年比 +200）。CF にも熱心に出ていて 1 回薄赤タッチしていた。構築が非常に得意。謎の実装問をいつの間にか通していることも多々ある。とても頼りになる。
miscalculation53：筆者。AtCoder のレートが 2000 くらい（昨年とほぼ変わっていない←え？）。他の 2 人に比べると ABC が得意で知識ドリブンのアプローチをすることが多い。

他 2 人が真っ当に ad-hoc が得意なのに対して私は機械的な解き方のほうが好きだったりといい感じに特性が分かれていたり、競プロへのモチベが大体同じくらいだったりして（所属が同じだから忙しい時期なども被りがちだし）、相性は結構いいチームだと思っている。

1 年間の取り組み

昨年も同じチームで参加したが国内予選で敗退し、とても悔しかった。そこから 8 月までは 3 人とも院試の勉強で忙しかったが、院試の終わり際に SSRS さんからこんな誘いがきた。

というわけでいつもチーム練をしていた工学部 6 号館で、都合がつく人で集まって CF Div.1 ばちゃをやっていた。レッドコーダーの頭脳をめちゃくちゃ贅沢に使わせてもらってかなり最高の時間だった。強い人が何考えてるか聞くと 1 人で upsolve するだけでは気づけなかった視点が得られて非常に素晴らしい。私以外の 2 人はおそらくこれのおかげもあってレートが上がっていて、私はレートこそ上がっていないもののできることは増えているはず（だと信じたい）。SSRS さん本当にありがとうございます。

あとは同時期に UC にも出始めた。UC は難しすぎるという噂を聞いていたがこれはかなり回によっていて、難しいときは手も足も出ないこともあるものの、黄 * 3 くらいでも十分楽しめるくらいの難易度であることのほうが体感多い気がする。これでチーム練をたくさん積んだことによってお互いの特性や得意不得意、チーム戦での立ち回りなどについてかなり理解が深まったと思う。

国内予選が近づいてからは、CF Gym で見つけた 3h セットをよく走っていた（過去の国内・模擬国内は昨年の練習でほぼ消費していたため……）。我々 3 人チーム vs SSRS さんソロで 3h セットを並走したりも数回した。ただ、そもそも 3h セットが少ない上に、難易度順でなかったり国内と傾向がだいぶ違ったりといった点でも困っていて、国内の対策になっているかは少し不安でもあった。

CF ばちゃ・チーム練のどちらも、暇なときはだいたい週 1 くらいだったが、卒論等で忙しかったりして自然消滅する時期もあったので、平均すると 1.5 〜 2 週に 1 回くらいのペースだったかな？

戦略

ICPC 攻略法：国内予選編 - クマーの競プロ精進日記を読んで、ほとんどの場合 2 人以上でやる、という部分に非常に共感したので、その戦略をとることにした。これでいくつか 3h を走ったところ割と手応えがよかったので本番もこれでやることにした。結果的に本番でもこれが守られていて、実際にうまくいったのでよかったと思う。

本番直前

模擬国内

模擬国内ではかなりうまくいって全体 7 位、現役内 4 位だった。しかし序盤のペナが多い、構文解析が苦手、などの課題も見つかった。

ペナについては、序盤でも慎重に行き、一瞬だけでも誰かの目は必ず通すことにしようと決めた。

構文解析については直前のチーム練でも出てきていて、うちのチームは confeito に丸投げすることにしていたのだが、彼が時間がかかっている間他 2 人が完全に蚊帳の外なのは割と問題があると感じた。そこで私が個人的に構文解析を練習した。（ICPC に出題されてみんな解くような範疇の）構文解析なら 1-2 時間で余裕で習得可能であることが判明して、これなら全然今までやっておけばよかったと思った。出題されなくても不安要素の払拭になったのでこれはやってよかったと思う。

東大内の枠争いについて

東大チームがなぜか誰もメンバー情報を書き込まないが、実は東大内では誰がどこにいるかはお互い完全に把握していた*1。チームメンバーのレート的に完全に格上なのは 217 と SSQS の 2 チームで（この 2 チーム間の比較もよくわからないが私は勝手に同じくらいかなと思っている）、あとはレート的に同格くらいのチームもいくつか、といった情勢で、217 と SSQS 以外に勝てば学内 3 位で通過できるかな〜とか言っていた。一方で、東大内で最もチーム練を（今回のメンバーで）してきたのは自分たちだろうとも思っていたので、単なるチームレートにとどまらないチーム戦の練度といった点でアドをとっていきたい、あわよくば 217 や SSQS にも勝ちたいとも考えていた。

環境構築

東大の ICPC 国内予選では基本的に学内にある ECCS 端末を使うことになる。これが結構曲者で、競プロ目的だと実質的に macOS しか使えないのと（これだけならまだよいが）、何かをインストールしようとするたびに管理者権限を要求されるのであらゆるものが入れられない。特に clang しか使えないのと VSCode の C/C++ 拡張がまともに動かず補完がきかないのがかなり困る。

clang については #include <bits/stdc++.h> がそのままでは使えないという問題がある。これは bits/stdc++.h のファイルをそのまま持ってきて -I オプションでインクルードすることで解決した（これは昨年からだが）。また、oj-bundle がそのままでは動かないようだ（よくわからなかった）。いろいろ試行錯誤したが、結果的に tatyam さんのツイートにある -E オプションで展開する方法を使うことで解決した。

( echo -n "#include <bits/stdc++.h>"; clang++ -nostdinc -fdirectives-only -E -P a.cpp ) > expand.cpp
で展開ができる！ https://t.co/fVLLMndyNo
— tatyam (@tatyam_prime) 2025年6月30日

補完については妥協して、"editor.wordBasedSuggestions" だけ動くようにした。後で聞いた話によると C/C++ 拡張をアンインストールして clangd をインストールするとうまくいったらしい。

このように環境が特殊なので、環境構築をした後は環境に慣れるために ECCS 端末で簡単めの 3h セットを走った。これはかなりやってよかったと思う。

またこのような状況なので、自前の端末を使用することにしたチームもあったようだ。これだと印刷機が（問題文の印刷以外で）使えなくなるという問題があったり、また単純に画面が小さいなどの不利益もあるので、総合的に判断した結果我々は ECCS 端末を使用することにした。

本番

始まる直前、私は緊張で心臓バクバクだった。他 2 人もそれなりに緊張していそうだった。でも緊張するということはそれだけ今まで練習を頑張ってきたということでもある。練習をまともにせず出た 2 年前とか一切緊張しなかったし。終わってからだから言えるのかもしれないが、このヒリヒリ感は案外悪くないと思う。

問題 PDF を開く。A を斜め読みし、B にスクロールさせて A を書き始める。テストケースの形式が今までの国内予選形式だったのは個人的に少し意外だった。ここでペナを出してもいけないので（bundle 後のコードが正しく動作するかも含めて）慎重に確認し、提出。AC (A 0:02)。

B を seren が書き、C を confeito が考える。私があまり概要を知らないのに変な口出しをしてしまってちょっとロスをしてしまったが通る (B 0:06)。

C を confeito が書き、D を seren が考える。私は C の見守りと D の考察の間くらいのことをする。ほどなく C も通る (C 0:12)。

D の考察を seren から聞き、それなら私が用意していたランレングス圧縮ライブラリを使うと実装が短縮できそうということで私が実装することに。テンプレに入れておいたグリッドの転置も役に立っていい感じだった。ただ正当性が怪しそうと感じたため「本当に大丈夫？」と 2-3 回くらい確認した気がする。不安だけど大丈夫な気がするなあなどと言いながら提出したが、WA が返ってきてしまう。

この間に E を考えていた confeito が解けたというので概要を聞き、その間に D を直す方法を考えてもらうことに。E は雰囲気正しそうと伝える。

D の反例と直す方法がわかったというので実装する。これで網羅できているかはそこまで自信がなさそうだったが、他に特に思いつかないので信用することにして提出する。これで WA だったら沼で嫌だな〜と思いながら提出すると通って安心した (D 0:29)。たしかこのあたりのどこかで印刷問題文がきたような気がする。

E を confeito が書き、F を seren が読む。私は E の見守りをしながら F を読んだりした。入力形式を間違えていることに提出直前に気づいたりしてかなりひやっとしたが、結果的に問題なく通って 3 位に浮上 (E 0:41)！このあたりでは順調だと感じていた。

このあたりではあんな難易度のセットだとは思いもしなかったので F に 3 人を割いていた。私も話を聞いていたが途中でよくわからなくなったので離脱して雛形を書くことにした。実際に操作をすると同時に出力すべき操作列を更新する関数を書いた。こういう構築はこれをやるとデバッグやランダムテストがしやすくなってかなりいいと思う。その間に解けたというので seren に実装を渡して、実装を見たりランレングス圧縮ライブラリの使い方を教えたりしていた。書けたようだが、怖いのでランダムテストを私が書いてから提出する。通る (F 1:05)。例年通りならもう通過できるだろう、早くコンテスト終わってくれ〜などと思っていた。

G は confeito が解けそうと言っていた。一瞬 3 人で見ていたが私は幾何の図が見たくなさすぎて逃亡して H を読んで考えていた。その間も G の実装をチラ見して気になったことを伝えたりした。たとえば 10'000'000'000 と書いていたが LL つけなくて大丈夫？とか、あまりをとっているところ負になる可能性はない？とか。これらはもしかしたら結果的に何も変わらないのかもしれない（変わるのかもしれない）が、こういう場面（書き方 1 と 2 があって、私は普段 1 を使っているが 2 でも大丈夫そうな気はしていて、今 2 で書かれている）はすべて口を出して、すべて安全側の 1 に倒すという方針にすることにしていた。実際今までこれを言い渋ってペナったことはたくさんある（前日の練習でも踏んだし、負の除算は昨年の G で実際に踏んだ苦い経験がある）。これが効いたのかどうかはわからないが、G が無事通る (G 1:30)。

このときも早くコンテスト終わってくれ〜と思っていたが、H は簡単そうと感じていて、I も読んだ感じ実は簡単がありえそうな上に The Revenge of Shinchan が通していたため、まだ頑張らないといけないのか……と思って軽く萎えた記憶がある。そんなことを言っても仕方がないので H の考察の初手（偶奇と、連続しているところに行けたらだいたい OK）を 3 人で共有する。大枠はわかるけど細かい部分がなかなか詰められず、焦る。

途中順位表で追い抜かれまくっていてかなり焦った。でも順位表を見ていてもどうせ全員で H を見るという戦略は変わらないだろうということで、confeito の提案で順位表を見ないようにした。これをやったおかげで H の考察に集中できた面はあり、やってよかったと思う。

H は結局「2 連続以上に到達できるかどうか」みたいな bool 配列を作っておくとよさそうという話になった。配列の作り方を 2 人が議論していたがよくわからなくなったので、自分はサンプルを眺めてその配列や答えを手計算して、その方法で本当に正しいかを確かめることにした。これのおかげでこの配列を作るパートのデバッグがかなりスムーズにできた上に、答えを求めるパートの実装（私がやった）も比較的スムーズにできた。というか D, F に続いて H でもランレングス圧縮ライブラリが大活躍で、ランレングス圧縮多すぎない？結果的に少し時間がかかってしまったが、無事ノーペナで AC (H 2:15)。

これで通過が確定してほしいところだったが、順位表を見ると I も結構通っていて、もし RecEight あたりが全完した場合落ちてしまう状況だった。こんなふうにこのコンテスト、AC して「これは通過だろ」→「えーまだ考えないといけないのか……」がずっと続いていて本当に苦しかった。I を考えるけど手がかりがあまりつかめない、そもそも permutation じゃない場合があるのやばくない？となる。実はコストがペアの距離の和とかだったりしない？と適当を言ったところで、これってあの 321 の嘘転倒数のやつに似てるよねという気持ちになって、問題そのものがなんか転倒数風味がするみたいなことを言う。このあたりのどこかで seren が、同種を swap しないからマッチするペアが簡単にわかって permutation の場合に帰着できる、ということに気づいて、そうじゃん賢すぎ、となる。その後しばらく考えていると confeito が「これって線分の交差数じゃない？」と言い出した。え、めちゃくちゃそれっぽい……！いくつか例を見てみても正しそう。これで正しかったら Rectangle Sum で解けますねと私が指摘して、残り時間も少ないし正しそうな気がしていたので、実装することにした。弦の交差の条件覚えてないな……と思って 2 人に投げてその間にペアを決めるパートの実装をしていたけど、結果的にこれは担当逆のほうがよかったかもしれない。交差の条件を Rectangle Sum に落とすパートで少しぐだった上に、Rectangle Sum ライブラリの使い方も間違えていて*2ぐだってしまった。これがすぐ書けないのは反省だな……。それでも間に合わないほどは遅くはならなくて、終了 5 分前に投げる。AC して通過が確定 (I 2:55)！めちゃくちゃ嬉しかったと同時に開放感がすごかった。

結果的には I が通っていなくても通過してはいたのだが、全完できない上に 10 位以内に入れないが学内 3 位なのでセーフ、だとしたらかなり後味が悪かっただろうから、I を通せて本当によかった。I は特に 3 人の考察が全部効いてきていてこれぞチーム戦、という感じだったのもとてもよかった。

おわりに

ついに念願の国内予選通過を果たすことができた。コンテストとしては、チーム戦らしい完璧に近い立ち回りができて、実力が発揮できて本当によかったとともに、チーム戦の面白さを実感した。B2 くらいの暇だった頃に比べると忙しくなってはいるのだが、その合間を縫ってこの 1 年間 ICPC のために 3 人 + SSRS さんの協力で頑張ってきた甲斐があったなと思う。とはいっても、まだまだ ICPC はこれからなので、さらに精進して、赤がいるようなチームとも渡り合えるような力をつけていきたい。横浜で会う皆さんよろしくお願いします。

*1:正直、めちゃくちゃメンバー言いふらしたいのを我慢していたし、今もしている

*2:sum クエリを追加するときにクエリ番号を返す仕様にしていたのだが、これを取得した sum と誤認していた。クエリ番号返すのやめて void にしようかな。本来補完がまともに使える環境なら関数の説明が表示されるので絶対にこの間違いをすることはないのだが……

2024-07-25

LIS になる列の構造

概要

数列の各要素について「LIS に使われる可能性があるか、使われる場合 LIS の何番目か」を計算しておくといろいろ便利です。

前提

増加部分列は「値」というよりは「添字」をとってきたものと思うのが見通しがよいです。この記事では次のように、増加部分列を添字の列として定義します：

長さ $N$ の数列 $A_0, \dots, A _ {N-1}$ の増加部分列とは、添字の列 $i_0, \dots, i _ {\ell-1}$ であって、 $(0 \leq) \ i_0 \lt \dots \lt i _ {\ell-1} \ (\leq N-1)$ かつ $A_{i_0} \lt \dots \lt A _ {i _ {\ell-1}}$ を満たすもの。最長増加部分列 (LIS) とは、増加部分列のうち、長さ $\ell$ が最大のもの。

また、LIS 長を求める $2$ 種類の DP（二分探索、セグ木）は既知として進めます。

本題

まず、添字 $i$ が LIS に使われる場合、その LIS 上での位置は一意です（そうでないとしたら、より長い増加部分列がとれて矛盾）。

$\mathrm{idx}' [ i ] :=$ 列 $A_0, \dots, A_i$ の増加部分列のうち $i$ を含むものの長さの最大値 ${} - 1$

とすると、添字 $i$ が LIS に使われる場合の LIS 上での位置は $\mathrm{idx}' [ i ]$ に一致します。

ところで、LIS に絶対に使われない添字が存在することもあります。そこで、 $\mathrm{idx} [i ]$ を次のように定義します：

添字 $i$ が使われる LIS が存在する場合、 $\mathrm{idx} [i ] := \mathrm{idx}'[i]$ とする。
添字 $i$ が使われる LIS が存在しない場合、 $\mathrm{idx} [i ] := -1$ とする。

また、 $0 \leq j \leq \ell ^ * -1$ （ $\ell ^ *$ ：LIS 長）に対して $\mathrm{cand}[j]$ を、 $\mathrm{idx}[i] = j$ を満たす $i$ たち（つまり、LIS の $j$ 番目になりうる添字の候補）を昇順に並べた列とします。

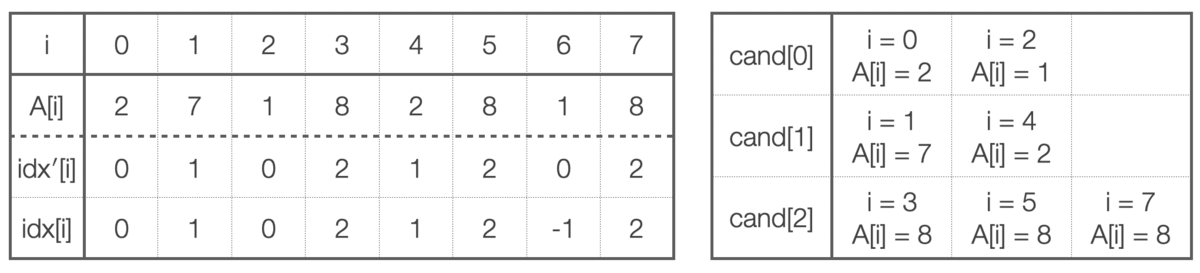
この $\mathrm{idx}$ （と $\mathrm{cand}$ ）を求めて、LIS の性質に関するいろいろな問題に応用するのが今回やりたいことです。

$\mathrm{idx, cand}$ の性質

（記法の補足： $\mathrm{cand}[j][-1]$ は $\mathrm{cand}[j]$ の末尾要素を表すとします。）

LIS は必ず、 $\mathrm{cand}[j]$ それぞれから $1$ つずつ選んできてできる列のどれかです。ただし、そのような列が必ず LIS になっているわけではありません。
の中身は添字の昇順ですが、これは値の降順になっています。つまり、です。
- そうでないと仮定すると、LIS より長い増加部分列がとれてしまいます。
それぞれの先頭をとってきた列は LIS です。つまり、かつです。これは添字の辞書順最小、値の辞書順最大の LIS です。
- 添字が単調増加でないと仮定すると、ある $j$ が存在して $\mathrm{cand}[j][0] \geq \mathrm{cand}[j+1][0]$ となりますが、 $\mathrm{cand}[j][0] \lt \dots \lt \mathrm{cand}[j][-1]$ より $\mathrm{cand}[j+1][0]$ が使われる LIS が存在しないことになり、矛盾します。
- 値が単調増加でないと仮定すると、ある $j$ が存在して $A _ {\mathrm{cand}[j][0]} \geq A _ {\mathrm{cand}[j+1][0]}$ となりますが、 $A _ {\mathrm{cand}[j+1][0]} \geq \dots \geq A _ {\mathrm{cand}[j+1][-1]}$ より $\mathrm{cand}[j][0]$ が使われる LIS が存在しないことになり、矛盾します。
それぞれの末尾をとってきた列は LIS です。つまり、かつです。これは添字の辞書順最大、値の辞書順最小の LIS です。
- 増加部分列になっていることの証明は上と同様です。
上記の辞書順最小・最大の LIS の性質より、辞書順最小 [resp. 最大] の LIS は、列を反転したときの辞書順最大 [resp. 最小] になります。

$\mathrm{idx, cand}$ の求め方

$\mathrm{idx}'$ は LIS 長を求める DP と同時に求めることができます（二分探索・セグ木のどちらのバージョンでも OK、簡単なので略）。

さて、 $i$ を含む LIS が存在する（ $\mathrm{idx}[i] \neq -1$ である）ための必要十分条件は、次のいずれかを満たすことです：

$\mathrm{idx}'[i] = \ell ^ * - 1$
ある $i _ \mathrm{nxt}$ が存在して、 $i \lt i _ \mathrm{nxt}, A_i \lt A _ {i _ \mathrm{nxt}}, \mathrm{idx}'[i] + 1 = \mathrm{idx}[i _ \mathrm{nxt}]$

この事実を用いると、 $\mathrm{idx}'$ を利用して $\mathrm{idx}, \mathrm{cand}$ が $O(N)$ 時間で計算できます。 $i$ を後ろから見つつ、各 $j$ について「今まで見た $i _ \mathrm{nxt}$ のうち $\mathrm{idx}[i _ \mathrm{nxt}] = j$ である最小の（つまり、 $A _ {i _ \mathrm{nxt}}$ が最大の） $i _ \mathrm{nxt}$ 」を管理していけばよいです。（なお下の実装例では、これを管理するついでに $\mathrm{cand}$ を求めています。）

実装例

#include <algorithm>
#include <vector>
using namespace std;

// idx[i] := A の i 番目が LIS に使われ得るなら LIS の何番目か、使われ得ないなら -1
// cand[j] := LIS の j 番目になりうる A の要素の添字の配列 (添字の昇順、値の降順)
// cand[j].front() たちをとってきたもの: 添字の辞書順最小、値の辞書順最大の LIS
// cand[j].back()  たちをとってきたもの: 添字の辞書順最大、値の辞書順最小の LIS
struct LongestIncreasingSubsequence
{
  vector<int> idx;
  vector<vector<int>> cand;

  LongestIncreasingSubsequence() {}
  template <class T>
  LongestIncreasingSubsequence(const vector<T> &a) : idx(a.size())
  {
    // LIS 長を求める DP (ここで idx' を求める)
    const int n = a.size();
    vector<T> dp;
    for (int i = 0; i < n; i++)
    {
      auto it = lower_bound(dp.begin(), dp.end(), a[i]);
      idx[i] = it - dp.begin();
      if (it == dp.end())
        dp.emplace_back(a[i]);
      else
        *it = a[i];
    }

    // idx, cand を求める
    const int len = dp.size();
    cand.resize(len);
    for (int i = n - 1; i >= 0; i--)
    {
      if (idx[i] == len - 1 || (!cand[idx[i] + 1].empty() && a[i] < a[cand[idx[i] + 1].back()]))
        cand[idx[i]].emplace_back(i);
      else
        idx[i] = -1;
    }
    for (auto &candj : cand)
      reverse(candj.begin(), candj.end());
  }
};

問題例

ABC354 F - Useless for LIS

LIS に使われうる要素をすべて求めてください。

解答

$\mathrm{idx}$ の求め方の一部そのままです。

Library Checker - Longest Increasing Subsequence

LIS をひとつ復元してください。

解答

$\mathrm{cand}[j]$ それぞれの先頭・末尾をとってくることで、辞書順最小・最大が復元できます。

yukicoder No.1804 Intersection of LIS

LIS に必ず使われる要素をすべて求めてください。

解答

$\mathrm{cand}[j]$ の要素が唯一であるところが答えになります。解説は「辞書順最小と辞書順最大の共通部分」という書き方をしていますが、同じことです。

ABC360 G - Suitable Edit for LIS

整数列の $1$ 要素を他の整数に書き換えて、LIS 長を最大化してください。

解答

$A$ の先頭に $-\infty$ を、末尾に $\infty$ を付け加えておきます。LIS 長を $1$ 増やせるための必要十分条件は、ある添字 $i_1, i_2$ が存在して、 $\mathrm{idx}[i_1],\mathrm{idx}[i_2] \neq -1, \mathrm{idx}[i_1] + 1 = \mathrm{idx}[i_2], i_2 - i_1 \geq 2, A _ {i _ 2} - A _ {i _ 1} \geq 2$ となることです。

$i_1$ を全探索します。 $i_2$ としてありうるのは、 $j := \mathrm{idx}[i_1] + 1$ として $\mathrm{cand}[j]$ の要素のどれかです。 $\mathrm{cand}[j]$ 内では添字が昇順、値が降順になっていることに注目すると、 $i_2 = \mathrm{cand}[j][k]$ が条件を満たすような $k$ の集合は区間になります。よってこの区間を二分探索か尺取り法（ $i_1$ を $\mathrm{cand}$ に現れる順番で探索すれば尺取りできます）で求めればよいです。

yukicoder No.992 最長増加部分列の数え上げ

LIS の個数を（適当な mod のもとで）数え上げてください。（列は添字が異なれば区別します）

解答

DP をします。

$\mathrm{dp}(j, k) :=$ LIS の $[0, j)$ 番目を決めて、なおかつ $j-1$ 番目を $\mathrm{cand}[j-1][k]$ とするような方法の数

$\mathrm{cand}[j]$ 内では添字が昇順、値が降順になっていることに注目すると、配る DP で考えた場合は配る先が区間に、貰う DP で考えた場合は貰う先が区間になります。いずれにしても、この区間を二分探索か尺取り法で求めて累積和や imos 法を利用すればよいです。

答えが $\displaystyle \prod _ {j=0} ^ {\ell ^ * - 1} \left|\mathrm{cand}[j]\right|$ にはならないことには注意してください。

なお、もし「値が同じであれば添字が異なっても同じ列とみなす」という設定だった場合は結構面倒になりますが、部分列 DP のように考えればなんとかなります（略、後で追記するかも）。

「みんなのプロコン」本選 D - KthLIS

辞書順 $K$ 番目の LIS を求めてください。（リンク先の問題では値の辞書順・値が同じであれば同じものとみなすという設定ですが、以下では簡単のため添字の辞書順で考えます）

解答

数え上げの DP と同じことをします。ただし、その後に辞書順 $K$ 番目を求めたいので、後ろから DP します。

$\mathrm{dp}(j, k) :=$ LIS の $[j, \ell ^ *)$ 番目を決めて、なおかつ $j$ 番目を $\mathrm{cand}[j][k]$ とするような方法の数

このテーブルを求めた後は、テーブルの情報にしたがって答えを前から決めていくことができます。

ところで、テーブルに載せる数が非常に大きくなる場合があります。これは、 $K$ との min をとった値を計算することにすれば対処できます。モノイド $\min(x + y, K)$ の区間積だと考えて、セグ木に載せることで計算できます（追記：尺取りになることを考えると SWAG でもできますね）（ところで、このモノイドは逆元がないので累積和だとうまくいかない気がするのですが、解説には累積和と書いてあるのでできるのかもしれないです。ちゃんと読んでいないのでよくわかりません）。

2024-07-06

ICPC 2024 国内予選参加記

くやしい〜〜〜〜〜〜
— 🌊 miscalc 🌊 (@miscalc53) 2024年7月5日

メンバー紹介

チーム名：Magical Fish

全員計数工学科数理コース 4 年の同学科・同学年チーム。以下筆者の主観による評価：

confeito：順当にチームで一番強い。難しい問題が解けるときはこの人のおかげであることが多い。幾何・構文解析・JOI 典型あたりを担当。
serendipity_：構築が特に得意。それ以外も割とバランスよくできる。実装力も結構あり、安心して実装を任せられることが多め。早く黄色なれ！
miscalculation53：筆者。他 2 人よりテンプレートやライブラリの整備をしていたり、言語知識を多めに持っていたりと、何かと知識枠の立場になりがち。一応数え上げ担当。

本番まで（チーム練・模擬国内）

去年は confeito・miscalc・magsta の 3 人だったが magsta が一旦競プロから距離を置くとのことで、3 月下旬に現メンバーで確定。

5 月中旬あたりからチーム練を始めた。チーム練はだいたい週 1 ペースで、工学部 6 号館*1の空き教室に集まって過去の国内・模擬国内を解いていた。この過程で、メンバーの得意不得意がある程度わかってきて、戦略も徐々に固まっていった。

過去の国内・模擬国内では割といい成績を出せていたと思っていたが、本番 1 週間前の模擬国内でめちゃくちゃ冷えて悲しい気持ちになった。もしかして昔の問題って今基準だと簡単？

本番直前

前日には本番で使う PC の環境を（テンプレート・ライブラリ等含め）結構頑張って整えた。（が、結局あまり役に立たなかったかも）

選抜ルールも前日に発表された。当初の想定通り横浜に行くには全体 10 位以上 or 学内 3 位以上が必要だが、例年は結局実質全体 10 位がラインだから今年もそうだろうと話をしていた。しかし……？

本番

A (2:48)：miscalc

B (10:19)：seren　見てない

C (19:59)：confeito　見てない

D (45:41)：miscalc　B, C の実装中に解法がわかったが、実装で結構もたついてしまった。とはいえ、なんとか持ち直して許容範囲におさめた気はする。実装する前に自分の周期性ライブラリを貼るのもちょっと考えたけど無限遠の扱いとかあるしな……と思い棄却、でも使った方がよかった可能性はある。一般に、このように一から書くかどうか微妙なときにどうするかは難しい……。

E：seren　（問題は）見てない、D でバグらせている間に解法がわかっていてすごい。

E の実装中に F を confeito と一緒に少し考えていたが、1 人でできそうな感じだったので離脱して G, H を読む。G も seren が得意そうな構築、H は全くの不可能ではないかもしれないが時間的に厳しそう、という印象になる。G を少し考えている間に E が通りそうになり、2 ペナはしたものの通る。

E (1:19:30)

F は confeito が実装できそうだったので、その間に G を seren と 2 人で考える。結局 99% くらい seren が解く。

F が炎上してそうだったので G に交代。解法が半分くらいしかわかっていないが DP にやや慣れている自分が骨組みと DP だけ書き、残りを seren が書く。19 時前には通せそうかなと思っていたが、色々バグっていてその特定に時間がかかってしまった。

G (2:50:11)

残り 10 分で confeito が F を実装、サンプルも試さずに提出しようとするが数秒間に合わず（結局サンプルがあっていなかったので、提出が間に合っていたとしてもだめだった）。

終了。ずっと見ていなかった順位表を見る。6 完 24 位。10 位は 7 完早解き……かと思いきやよく見ると学内 3 位のほうが下であり、時間ぎりぎりでも 7 完できていれば全然可能性があったという結果。悔しい……。

感想

（昨年比）割と練習してきたし、あと 1 完できていれば通っていたかもしれないと考えるとかなり悔しい。F と G のどちらかでもう少しバグっていなければ……。

こういう、自分が担当する範囲の問題があまりないときの立ち回りは個人的にチーム練のときからずっと課題だが、今回も貢献が少なくなってしまってチームメイトに申し訳ない。F もうちょっと見るべきだった？ G 解法をちゃんと理解していれば seren が書いているときにバグを指摘できた？などいろいろ後悔がある。

実は来年ラストイヤーらしい（1, 2 年、コロナ等で知り合いが少なくてチーム組めなかったので、全く実感がないが……）。悔いの残らないように真っ当に実力をつけて帰ってきます。

*1:計数の授業はだいたいこの建物で行われる

2024-04-21

floor に関する等式の証明

最近気づいたので書きます（有名かも？）

有名な等式として $\displaystyle \left\lfloor \frac{N}{ab} \right\rfloor = \left\lfloor \frac{\left\lfloor \frac{N}{a} \right\rfloor}{b} \right\rfloor$ （ $N, a, b$ は正整数）があります。これを証明します。

整数 $n$ と実数 $r$ に対して

$\begin{align} n \leq r \iff n \leq \lfloor r \rfloor \tag{ * } \end{align}$

であることを利用します。 $n$ を整数として

$\begin{align} &\phantom{{}\iff{}} abn \leq N \tag{1} \\ &\iff bn \leq \frac{N}{a} \tag{2} \\ &\iff n \leq \frac{N}{ab} \tag{3} \end{align}$

ですが、 $(3)$ の後でだけ $( * )$ を適用すると $\displaystyle n \leq \left\lfloor \frac{N}{ab} \right\rfloor$ が得られ、 $(2), (3)$ の両方の後で $( * )$ を適用すると $\displaystyle n \leq \left\lfloor \frac{\left\lfloor \frac{N}{a} \right\rfloor}{b} \right\rfloor$ が得られます。このふたつが同値で、右辺が整数であることから、右辺は等しいです。 $\square$

雑にいうと、操作の途中で floor をとったりとらなかったりしてよい、という感じです。 $\displaystyle \left\lfloor \sqrt{\frac{N}{i}} \right\rfloor = \left\lfloor \sqrt{\left\lfloor \frac{N}{i} \right\rfloor} \right\rfloor$ なども同様に示せますね。

2024-03-21

XOR の基底　事実・できることまとめ

間違っている部分やもっと簡単にできる部分などがあれば教えていただけると助かります。

この記事での記法など

XOR 演算子は $\oplus$ で書く。
非負整数の（有限）集合 $S$ に対して全体の XOR $\displaystyle \bigoplus _ {s \in S} s$ を $\mathrm{XOR}(S)$ とも書く。
非負整数の（有限）集合 $S$ に対して $X(S) = \{ \mathrm{XOR}(S) \mid T \subseteq S \}$ （何個か選んで作れる XOR 全体の集合）と書く。
$S$ を $\mathbb{F} _ 2$ 行列とみたときの基底（XOR 基底）の $1$ つを $B(S)$ と書く。
$S$ の要素はワードサイズに収まることを仮定する。ワードサイズを $w$ と書く。

本題

[1] 作れる XOR の種類数

$|X(S)| = 2 ^ {|B(S)|}$

[2] XOR を作る方法の数

$c(x) := \# \{ T \subseteq S \mid \mathrm{XOR}(T) = x \}$ とする。

$x \notin X(S)$ のとき、 $c(x) = 0$
$x \in X(S)$ のとき、 $c(x) = 2 ^ {|S| - |B(S)|}$

つまり、作れる XOR はどれも、作る方法の数が同じである。*1

F - Limited Xor Subset

No.2672 Subset Xor Sum - yukicoder

[3] 作れる XOR のうち、ある bit が立っているものの個数

その bit が立っている要素が $S$ にない場合、明らかに $0$
そうでない場合、その bit が立っているものと立っていないものは半々である。つまり、 $\# \{ x \in X(S) \mid \mathrm{test}(x, j) = 0 \} = \# \{ x \in X(S) \mid \mathrm{test}(x, j) = 1 \}$ である（ $x$ の $j$ bit 目を $\mathrm{test}(x, j)$ と表した）。
- 理由： $B(S)$ から選ばれる要素のうち、 $j$ bit 目が立っているものの個数の偶奇で分かれる。 $j$ bit 目が立っている要素を $1$ つ固定し、それを選ぶ・選ばないを flip することで全単射が作れる。

[4] chmin で XOR 基底を求めるアルゴリズム（いわゆる noshi 基底）

xor の掃き出しすごい簡単に出来るんですね

vector<int> basis;
for(int e : a){
for(int b : basis)
chmin(e, e ^ b);
if(e)
basis.push_back(e);
}

これで数列 a の基底が basis に入る
— 熨斗袋 (@noshi91) 2019年11月30日

このアルゴリズムを実行すると、msb*2 が distinct な基底が得られる。行列の言葉でいうと、（行を降順ソートすれば）階段行列になる。 $S$ の要素 $1$ つを処理するのに $O(w)$ 時間。

[5] 作れる XOR のうち $k$ 番目に小さいもの

[4] のアルゴリズムを少し変形すると、msb が distinct なだけでなく

msb は他の要素で立っていない（すなわち、 $b_i, b_j \in B(S), b_i \neq b_j$ ならば $\mathrm{test}(b_j, \mathrm{msb}(b_i)) = 0$ ）

を満たす基底が得られる（具体的なアルゴリズムはこの節の一番下にある問題の解説を参照）。行列の言葉でいうと、（行を降順ソートすれば）簡約行列になる。基底を計算するパートの計算量は [4] と同じ。

この基底をソートする（昇順に $b_0, b_1, \ldots, b_{m-1}$ とする）。すると、各 $b_i$ を選ぶか選ばないかを $01$ で表したものが $k$ の $2$ 進表記と対応する。すなわち、 $X(S)$ の要素を昇順に $x_0, x_1, \ldots, x _ {2 ^ m - 1}$ とすると、 $\displaystyle k = \sum _ {i = 0} ^ {m-1} c_i 2 ^ i \: (c _ i \in \{ 0, 1 \})$ のとき $\displaystyle x_k = \bigoplus _ {i = 0} ^ {m-1} c_i b_i$ となる。クエリ $O(w)$ 時間。

verify に使える・より詳細な解説が書いてある：G - Partial Xor Enumeration

[6] 作れる XOR のうち $v$ 以下で最大のもの（lower_bound や upper_bound のようなもの）

単純な二分探索で自明に $O(w ^ 2)$ 時間になるが、もっと高速になる。

[5] の基底をとる。基底を降順に見ていき、「選んでも $v$ を超えないなら選ぶ」ことを繰り返す。クエリ $O(w)$ 時間。

[7] 奇数個・偶数個選んで作れる XOR

今あるどの bit よりも上の余っている bit を $1$ つ選び、全部の値で立てておく。その bit が $0$ なら偶数個、 $1$ なら奇数個選んだといえる。 $X(S)$ を昇順に並べたとき、 $[0, 2 ^ {|B(S)|-1})$ 番目はこの bit が $0$ に、 $[2 ^ {|B(S)|-1}, 2 ^ {|B(S)|})$ 番目はこの bit が $1$ になる（[3] の事実も参照）。
$X _ {\mathrm{ev}}(S) := \{ \mathrm{XOR}(T) \mid T \subseteq S, |T| \equiv 0 \pmod 2\}$ （偶数個選んで作れる XOR の集合）と書く。 $S = \{ s _ i \} _ {0 \leq i \lt n}$ に対して $S' := \{ s _ 0 \oplus s _ i \} _ {1 \leq i \lt n}$ とすると、 $X(S') = X _ {\mathrm{ev}}(S)$ となる。

No.803 Very Limited Xor Subset - yukicoder

ARC のネタバレ注意

E - Rearrange and Adjacent XOR

[8] 作れる XOR のうち、 $x$ との XOR が $k$ 番目に小さいもの

今あるどの bit よりも上の余っている bit を $1$ つ選び、 $x$ のその bit を立てたものを $x'$ とする。 $S' := S \cup \{ x'\}$ を考えると、 $X(S')$ のうち先程新たに立てた bit が立っているもの、すなわち昇順で $[2 ^ {|B(S')|-1}, 2 ^ {|B(S')|})$ 番目のものが対応物（[3] の事実も参照）。
最大だけなら、後で扱う問題の解説に書いてある方法で求まる：[4] または [5] の基底を降順に見て、 $\mathrm{chmax}(x, x \oplus b _ i)$ を繰り返す。
任意の $k$ 番目で同様のことができるかは不明。

[9] 作れる XOR のうち、 $x$ との XOR が $v$ 以下で最大のもの

[8] 1. と [6] を組み合わせるとできる。

例題

G - Xor Cards

非負整数列 $(s _ i) _ {0 \leq i \lt n}$ と $(t _ i) _ {0 \leq i \lt n}$ が与えられる。 $I \subseteq \{ 0, 1, \ldots, n-1 \}$ を $I \neq \emptyset, \displaystyle \left( \bigoplus _ {i \in I} s _ i \right) \leq v$ のもとで選べるとき、 $\displaystyle \bigoplus _ {i \in I} t _ i$ の最大値を求めよ（あるいは、そのような選び方はないと判定せよ）。 $n \leq 1000, s _ i, t _ i, v \lt 2 ^ {30}$

（記号をこの記事用に変えています）

いったん $I = \emptyset$ を許して考える。

$u _ i := s _ i \cdot 2 ^ {30} + t _ i$ 、 $U := \{ u _ i\} _ {0 \leq i \lt n}$ とすると、求めるものは

$X(U)$ の $(v + 1) \cdot 2 ^ {30}$ 未満の要素のうち下 $30$ bit が最大のもの

となる。 $(v + 1) \cdot 2 ^ {30}$ 未満となる境界を [6] の方法で求める。 $r _ 0$ 番目が $(v + 1) \cdot 2 ^ {30}$ 未満で最大であるとすると、条件を満たす選び方に対応する $2$ 進数が、区間 $[0, r _ 0 ]$ になっている。つまり、境界を求めるのに使った [5] の基底の下 $30$ bit を取り直して $( t' _ i ) _ {0 \leq i \lt |B(U)|}$ とすると、求めるものは

$I' \subseteq \{ 0, 1, \ldots, |B(U)|-1 \}$ を、対応する $2$ 進数が区間 $[0, r _ 0 ]$ にあるように選ぶときの $\displaystyle \bigoplus _ {i \in I'} t' _ i$ の最大値

となる。（ここで $|B(U)| \leq 60$ であることが計算量的に効いてくる。）（ここで先程許した $I = \emptyset$ を考える。 $I = \emptyset$ 以外で条件を満たせないのは、 $r _ 0 = 0$ で、 $I' = \emptyset$ に対応する $I$ が $I = \emptyset$ の自明な $1$ 通りしかない場合。[2] より、 $n = |B(U)|$ かどうかで判定できる。）

$f(j, r, x) := ( t' _ i ) _ {0 \leq i \leq j}$ から、対応する $2$ 進数が区間 $[0, r ]$ にある選び方をしたとき、選んだ整数と $x$ の総 XOR の最大値とする。答は $f(|B(U)|-1, r _ 0, 0)$ である。 $j$ 番目を選ぶかどうかで場合分けして再帰する。

$\mathrm{test}(r, j) = 0$ のとき
- $j$ 番目を選んでしまうと $r$ より大きくなるので選べない。 $f(j-1, r, x)$ へ。
$\mathrm{test}(r, j) = 1$ のとき
- $j$ 番目を選ばないとき
  - 区間 $[0, 2 ^ j - 1 ]$ に対応。つまり $( t' _ i ) _ {0 \leq i \leq j-1}$ から好きに選んだときの選んだ整数と $x$ の総 XOR の最大値となる。これは [8] なので解ける。
- $j$ 番目を選ぶとき
  - 区間 $[2 ^ j, r ]$ に対応。つまり $t _ j$ を必ず選ぶとした上で、 $( t _ i ) _ {0 \leq i \leq j-1}$ から区間 $[0, r - 2 ^ j ]$ にある選び方をしたときの選んだ整数と $x$ の総 XOR の最大値となる。 $f(j-1, r - 2 ^ j, x \oplus t _ j)$ へ。

やっていることは公式解説と多分同じ（再帰をループで書いているだけ）。計算量も同じく $O(nw + w ^ 3)$ になる。

*1:教えていただきありがとうございます https://twitter.com/Sophia_maki/status/1766876738024300696

*2:most significant bit: 立っている最上位ビット

2024-02-25

Range Chmin Point Get

書いた動機

range chmin でググるとなぜか beats の話しかヒットしないので

区間 chmin 一点取得だけならもっと簡単にできます。（当たり前ですが chmin を chmax に替えても可）

ACL の遅延セグ木を使う

ABC179 解法 • knshnbのブログの F のようにすればできます。

区間積などを呼び出すと壊れますが、呼び出さないことで解決

双対セグ木

双対セグメント木 - HackMD あたりを読みましょう（面白いです）

問題例

2024-01-11

JMO 2017 予選 9 を母関数で解いてみた

競プロにもありそうな教育的な問題だと思いました。

問題

問題リンク

$1, 2, \ldots, 2017$ の並べ替え $\sigma = (\sigma(1), \sigma(2), \ldots, \sigma(2017))$ について、 $\sigma(i) = i$ となる $1 \leq i \leq 2017$ の個数を $F(\sigma)$ とする。すべての並べ替え $\sigma$ について $F(\sigma) ^ 4$ を足し合わせた値を求めよ。

解答

$a _ {n, m}$ を、 $F(\sigma) = m$ であるような $1, \ldots, n$ の順列 $\sigma$ の個数とします。

$m = 0$ のときは撹乱順列の個数で、包除原理から $\displaystyle a _ {n, 0} = \sum _ {k=0} ^ {n} (-1) ^ k \binom{n}{k} (n-k)! = n! \sum _ {k=0} ^ {n} \frac{(-1) ^ k}{k!}$ とわかります（母関数による導出もあります：指数型母関数入門 – 37zigenのHP）。

一般の $m$ に対しては、一致する箇所 $m$ 個を選んだ後、残り $n-m$ 個の場所で撹乱順列を作ると考えて、 $\displaystyle a _ {n,m} = \binom{n}{m} a _ {n-m, 0} = \frac{n!}{m!} \sum _ {k=0} ^ {n-m} \frac{(-1) ^ k}{k!}$ となります。

答えは $\displaystyle \sum _ {m=0} ^ n m ^ 4 a _ {n, m} = n! \sum _ {m=0} ^ n \frac{m ^ 4}{m!} \sum _ {k=0} ^ {n-m} \frac{(-1) ^ k}{k!}$ （で $n = 2017$ としたもの）です。

母関数を使って考察します。まずは撹乱順列の個数 $\displaystyle \sum _ {k=0} ^ {n-m} \frac{(-1) ^ k}{k!}$ の母関数を考えましょう。 $\displaystyle \frac{(-1) ^ k}{k!} = \lbrack x ^ k \rbrack e ^ {-x}$ であり、撹乱順列の個数はその累積和なので $\displaystyle \frac{1}{1 - x}$ をかけたものが母関数になります。つまり $\displaystyle \sum _ {k=0} ^ {n-m} \frac{(-1) ^ k}{k!} = \lbrack x ^ {n-m} \rbrack \frac{e ^ {-x}}{1 - x}$ です。

次に $\displaystyle \frac{m ^ 4}{m!}$ の母関数を考えましょう。このままでは考えにくいので、 $m ^ 4 = m + 7m(m-1) + 6m(m-1)(m-2) + m(m-1)(m-2)(m-3)$ と変形します（このように冪乗を下降冪の級数で表したときの係数は第 2 種スターリング数です）。すると

$\begin{align*} \frac{m ^ 4}{m!} &= \frac{1}{(m - 1)!} + \frac{7}{(m - 2)!} + \frac{6}{(m - 3)!} + \frac{1}{(m - 4)!} \\ &= \lbrack x ^ {m-1} \rbrack e ^ x + 7 \lbrack x ^ {m-2} \rbrack e ^ x + 6 \lbrack x ^ {m-3} \rbrack e ^ x + \lbrack x ^ {m-4} \rbrack e ^ x \\ &= \lbrack x ^ m \rbrack ( x e ^ x + 7 x ^ 2 e ^ x + 6 x ^ 3 e ^ x + x ^ 4 e ^ x) \end{align*}$

となります（負の階乗の逆数や負冪の係数は $0$ とみなしておきます）。よって答えは

$\begin{align*} &\phantom{{}={}} n! \sum _ {m=0} ^ n \frac{m ^ 4}{m!} \sum _ {k=0} ^ {n-m} \frac{(-1) ^ k}{k!} \\ &= n! \sum _ {m=0} ^ n \lbrack x ^ m \rbrack (x + 7 x ^ 2 + 6 x ^ 3 + x ^ 4) e ^ x \cdot \lbrack x ^ {n-m} \rbrack \frac{e ^ {-x}}{1 - x} \\ &= n! \lbrack x ^ n \rbrack \frac{x + 7 x ^ 2 + 6 x ^ 3 + x ^ 4}{1 - x} \\ &= n! \lbrack x ^ n \rbrack (x + 8 x ^ 2 + 14 x ^ 3 + 15 x ^ 4 + 15 x ^ 5 + 15 x ^ 6 + \cdots) \\ &= 15 \cdot 2017! \end{align*}$

となります。（補足：2 行目から 3 行目は FPS の積の定義、3 行目から 4 行目は $\displaystyle \frac{1}{1 - x}$ 倍が累積和）

競プロ

$2017$ を $n$ に、 $4$ を $d$ に一般化したときの答えを $\mathrm{ans}(n, d)$ とすると、 $\displaystyle \mathrm{ans}(n, d) = n! \sum _ {k = 0} ^ {\min(n, d)} S(d, k)$ です（ $S(\cdot, \cdot)$ は第 2 種スターリング数）。これを（mod 998 とかで）計算する競プロの問題だと思うことにします。[多項式・形式的べき級数] 高速に計算できるものたち | maspyのHP を参考にすると、次のことがわかります。

$D$ 固定、クエリ $n$ に対して $\mathrm{ans}(n, D)$ を求める：「第 2 種 Stirling 数」の項の「前者」の方法で $S(D, 0), \ldots, S(D, D)$ を $O(D \log D)$ で前計算して累積和をとることで、各クエリについて（階乗の計算を除いて） $O(1)$ で求まる。
$N$ 固定、 $d = 0, 1, \ldots, D \ (D \leq N)$ に対して $\mathrm{ans}(N, d)$ を求める： $S(d, k)$ がすべての $k = 0, 1, \ldots, d$ について足されることから Bell 数になって、 $O(D \log D)$ で求まる（「Bell 数」の項も参照）。
$N$ 固定、 $d = 0, 1, \ldots, D$ に対して $\mathrm{ans}(N, d)$ を求める：「第 2 種 Stirling 数」の項の「後者」を参考にすると $\displaystyle \sum _ {k=0} ^ {\min(N, D)} \frac{1}{k!} (e ^ x - 1) ^ k$ を $D$ 次まで求めればよい。これは $\displaystyle \sum _ {k=0} ^ {\min(N, D)} \frac{1}{k!} x ^ k$ を Polynomial Taylor Shift した後 $e ^ x$ を代入すればよいので（「Polynomial Taylor Shift」および「特殊な合成」の項を参照）、（階乗の計算を除いて）全体 $O(D \log ^ 2 D)$ で求まる。